A large literature of alternative interpretations exists, including but not limited to:
These interpretations vary in their degree of realism. The Copenhagen Interpretation eschews realism, but doesn't replace it with anything--Bohr in particular seems to sometimes say that the quantum world simply does not exist, which is clearly unacceptable: something gives rise to phenomena, and whatever that is, is what exists.
The Many Worlds and Quantum Potential interpretations, due to Everett and Bohm, respectively, are both realist theories: they say that the underlying reality is prepackaged into particular conceptual categories which we discover rather than invent. Such interpretations have great appeal to the realist intuitions we develop in everyday life, but they have failed to catch on in the physics community because the realities they describe are so blatantly pathological: Many Worlds requires an endlessly bifurcating reality, and the Quantum Potential requires us to believe in undetectable massive particles moving with infinite velocities. Neither of these accords well with the way physicists would like to describe reality.
Rather than offer yet another realist interpretation of quantum mechanics, as a conceptualist I'm interested in subverting the realist program altogether, yet still retaining the basic axioms of existence and identity. To do this, I first outline what I mean by "realism" and examine what the commitments of realism are in the context of a particular experiment in which Bell's Inequalities are violated. Having shown that realism is false, I then examine the commitments of conceptualism, particularly with regard to the axioms of existence, identity and consciousness, and with regard to the laws of thought. I discuss the role that the concepts of TIME and SPACE play in the axioms and laws of thought, and show that while it is possible for existence and identity to be non-local, our understanding of them must be local due to the nature of consciousness. From this it follows that there is an underlying reality that gives rise to quantum phenomena, but that it is largely unknowable by us.
...the world has a definite and mind-independent natural-kind structure...The issue for realism is not whether or not the world exists independently of minds, but whether or not the world is pre-structured into natural kinds, the discovery of which is the business of science. This means that common terms--terms referring to members of classes, have as their referents these natural kinds, as things in themselves rather than just as modes of existence that are picked out and grouped by a mind for some purpose. In terms of universals [Ray,1999]:In particular the metaphysical stance implies that if the unobservable natural kinds posited by theories exist at all, they exist independently of human's ability to know, verify, recognize, that they do. Instead of projecting a structure onto the world, scientific theories, and scientific theorizing in general, discover and map out an already structured and mind-independent world.
Realism is the theory of universals that takes the referents of common terms to be mind-independent existents over and above the objects themselves
So when a realist talks about atoms or photons or their properties, she is claiming that these things exist intrinsically, as kinds, independently of her interactions with them or awareness of them. Implied in the commitment to natural kinds is a commitment to determinate values, which I'll expand upon below.
Conceptualism is a theory of universals that takes the things named by general terms to be mind-dependent abstractions. These mental entities are based on similarities that the conscious subject notices between real objects.A conceptualist talking about atoms and photons and their properties, is therefore claiming that the terms "atom", "photon" and so on are names for categories that he has come up with to subsume various particulars based on similarities that are relevant to his purposes. His use of these categories and not others is a result of his purposes as much as it is a result of the reality he's categorizing.
Now, "being linearly polarized along the x-axis" is a general term: there are many photons that could have this property. So to a realist, there must be a real, mind-independent category that makes the attribution of this general property true by virtue of its exemplification relationship to it. To a realist, there is part of reality that "just is" a photon, independent of any knowing subject categorizing it that way, and that photon "just has" a linear polarization along the x-axis, independently of any knowing subject categorizing it that way. Furthermore, it must be the case, to a realist, that we do not have any choice as to how to categorize reality: the categories are given by and in reality.
Let's see how these commitments play out when applied to a real case.
Because of this, the only way the atom can decay is by emitting two photons whose angular momenta add up to zero. It turns out that this condition is only met when both photons have the same linear polarization. However, because the original system consisting only of the excited atom is spherically symmetric (this is one of the consequences of having zero angular momentum) there is no preferred direction for the common plane of polarization of the two photons. That is, they must have the same plane of polarization, but there is nothing about the system that causes that plane to be one plane rather than another. The identity of the plane appears to be ambiguous.
Thus far, the commitment to realism in the description above has been mostly implicit, and simply a consequence of the fact that natural language has a heavily realist bias. Now, however, a realist must make an explicit commitment: the common plane of polarization is part of the identity of the individual photons. It must be possible to talk about this property of the photons independently of any mind that might want to categorize this part of reality as photons, or, having made that categorization, wanting to know what their polarization might be. The property "having a linear polarization along a particular plane" is something the photons must possess in a realist's view, because on that view things exist in categories independently of anyone who categorizes, and a part of reality that bears an exemplification relation to the category "photon" and bears an exemplification relation to the category "linearly polarized" must also bear an exemplification relation to the category "linearly polarized along some particular plane."
Realism does not allow indeterminate identity: to be a member of a particular category is to have a determinate value along the dimension that category names.
As a final consideration, let us assume that the events described above happen many times: the atom gets re-excited after it emits a pair of photons, and then decays again emitting another pair, and so on, for as long as we want.
So the realist's claims amount to this:
Remember that by "real" in the above the claim is that not just that there are particulars that exist, but that there are particulars that exist as members of the categories that name them, and all that that implies. So to be a real photon is on this view to have a real polarization, independently of anyone categorizing the photon in a way that makes its polarization relevant or meaningful.
Because of this, if any of these claims are false, they are all false. If there is no real plane of polarization, then there is no real photon, because on the realist view identity must be independent of the identifier--there is no room within realism for things that are photons but that don't have any particular plane of linear polarization (readers with a background in quantum theory will realize that this means we don't have to do anything so elaborate as Bell's argument to rule out realism, as Heisenberg in particular was quite aware--the arbitrary choice of basis allowed by the quantum-mechanical formalism already implies that there is no preferred categorization of reality.)
So do the realist claims above commit us to anything that can be shown to be false? They do, and this is the nature of Bell's argument, which usually gets presented in the form of statistical inequalities. Here, however, I'm just going to point out the significance of the functional form of the results of measurements on the two photons.
Furthermore, once a photon has been transmitted through a polaroid, its plane of polarization has been changed to the match the orientation of the transmission direction of the polaroid, so if we put a second polaroid behind the first and orient it at a different angle, the total transmission probability is just the cosine of the angle between the two.
If the two photons in each of the pairs of photons emitted from the calcium atom have a common plane of polarization, and we set up two polaroid filters on opposite sides of the source so that one photon passes through one and one photon passes through the other (we assume for simplicity that the photons always travel in opposite directions, which is roughly correct) then we can predict what the correlation between them will be as a function of the angle between the transmission directions of the two polaroids.
In particular, when the two polaroids are oriented at 90 degrees to each other, we can say that there will still be photons that get through both polaroids about a half of the time. This is because the common plane of polarization, if there is one, is randomly oriented because the initial system is spherically symmetric, so each photon has a better than 50% chance of getting through its filter. There will be cases, for instance, when the common plane of polarization is at 45 degrees relative to both filters, which are at 90 degrees to each other. In these cases, both photons will be transmitted about 70% of the time (cos(45) = 0.707).
If realism is true, then we can be sure that when the filters are at 90 degrees to each other, there will still be cases where both the photons are detected. And conversely, when the filters both have the same orientation, we can be sure if realism is true there will still be lots of cases where one photon is detected and the other is not. A plot of the functional form is forthcoming.
So we have an empirical claim that allows us to test a metaphysical doctrine: do things exist with their identity fully specified relative to a set of predefined, mind-independent universal categories?
The answer is unequivocally, "No."
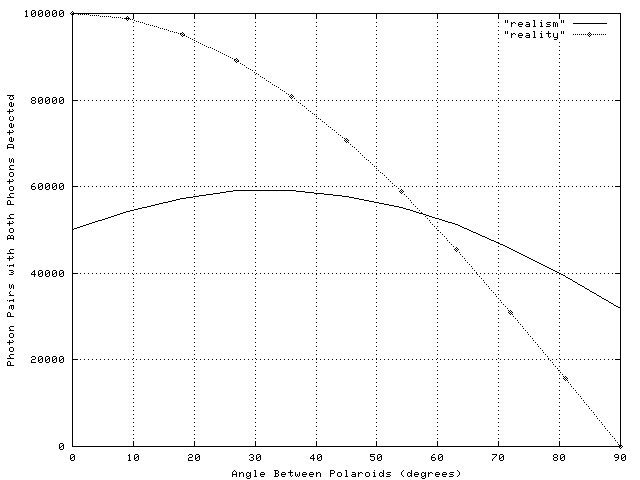
Experimentally, the functional form of the correlation between detections of the two photons is a cosine law: when the polaroids are at 90 degrees to each other, there are no pairs that have both members detected. When the polaroids are lined up with each other, the joint detection rate is 100%. There are of course non-ideal aspects to the experiments, however, the precise numerical agreement with the quantum-mechanical predictions for the experiments--which show a cosine law dependence--clearly rules out realism.
The difference between realism and reality for this experiment is shown in the figure below. Two polaroid filters are placed on either side of the calcium atom source, and they are set with an angle of zero between their transmission directions. Photons are detected coming from the source for a long enough time that we think 100000 pairs have been emitted, then one or both of the polaroids are rotated so that they have 10 degrees between their transmission directions and data are again accumulated, and so on.

If realism is true, then both photons in each pair must share a real common plane of polarization, and the number of pairs that have both photons detected will look like the "realism" curve in the figure: low at zero, peaking at around 30 degrees, and falling off again above, but never close to zero.
Unfortunately for realism, reality does not conform to realist expectations. There's a sense in which realists should be heartened by this: reality in fact behaves so weirdly that there's no doubt at all that there is a reality out there, independent of us! No subjectivist could ever dream up such strange behavior--this is akin to Descartes' argument that external reality must exist because otherwise he would not be able to conceive of anything greater than himself. If reality were not this way I'm sure no one would have suggested it. Ergo, there is a mind-independent reality, and it is not pre-packaged into categories or natural kinds.
The argument I've presented here is a concrete version of John Bell's much more general (but correspondingly more abstract and difficult for the non-physicist to appreciate) argument that shows that no realist account that does not assume there is an interaction between the widely separated photons can explain the data. That is, any realist account must say that once one photon interacts with a polaroid it must somehow influence the plane of polarization of the other photon to make the probability of detecting both photons dependent only on the angle between the polarizers. And to ensure angular momentum is conserved, this interaction must take place instantaneously, over arbitrarily large distances.
Another view of why realism can't account for the experimental results is to consider the nature of the cosine function. Realism assumes that there is a real common plane of polarization that is shared by both photons in each pair. This has the consequence that the probability of detecting a photon depends on the cosine of the angle between the polaroid it passes through and the direction of this real plane. So for each individual photon (call them photon 1 and photon 2, which pass through polaroid 1 and polaroid 2 respectively) the probability of detection is:
cos(theta-theta_i) [i = 1,2]where theta is the angle of orientation of the photon's plane of polarization and theta_i is the angle of orientation of the polaroid, where i is a variable index that can be 1 or 2 depending on which polaroid we are talking about.
The probability of detecting both photons in a pair is therefore equal to:
cos(theta-theta1)*cos(theta-theta2)which is just the product of the individual probabilities, according to the usual rules of probability calculus. This equation was used to generate the "realism" curve shown in the figure above by integrating over the angle theta using a simple Monte Carlo calculation to produce the average probability of detecting both photons in a pair as a function of the angle between the polaroids, theta1-theta2.
For the mathematically minded, one way of looking at the problem with realism is that there is no way of writing the equation that describes reality:
cos(theta1-theta2)in a form of the product of two independent functions, fa and fb:
fa(theta1,otherstuff1)*fb(theta2,otherstuff2)and so there is no way of reproducing reality with any theory that does not posit some instantaneous interaction between the two photons. The only way the product of two functions can be made to reproduce
cos(theta1-theta2)
is if the "otherstuff" in one of the functions depends
on the value of the other function,
and physically this dependence appears as instantaneous
communication between the photons. The communication
must be instantaneous if angular momentum is conserved,
and we have very good reason to believe it is.
My next task is to show why positing such an instantaneous interaction at a distance would be a bad move for a realist, and then to move on to a conceptualist view of this problem, jettisoning realist baggage as I go.
Before leaving the description of this experiment, let it be said that I'm intimately familiar with the issues surrounding experimental violations of Bell's Inequalities. I consider Aspect's "delayed choice" work to be definitive, and do not believe that any of the criticisms of it are sufficient to change its conclusions. In particular, some critics have pointed out that the two photons are not emitted at precisely the same time, as there is an intermediate state between them. If anything, this should make the results even more mysterious to the realist, who has to posit how the detection of one photon can affect the properties of another that hasn't even been emitted yet! And of course, such cavils are in any case not relativistically invariant--there are frames in which the second photon is always emitted after the first. And other work using parametric down-conversion as the source of photon pairs has addressed these and other quibbles more directly. So for the purposes of this discussion I take it as given that reality is correctly described by quantum mechanics, because in an entirely ordinary sense, this is in fact the case.
The task of conceptualism in this case is to ask: What can we say about reality? And in particular, what are the constraints that everything we say must conform to? And to what extent do those constraints come from reality, and to what extent do they come from our nature as knowing subjects? And most importantly, is there a difference between what we can say, and what exists?
The axioms of objectivism are usually given as something like:
Everything that exists, exists, the first axiom tells us. Everything that exists, exists in a particular mode, the second axiom tells us. That way may or may not have anything to do with the categories of space and time that we create based on our experiences. There is no reason to believe that, based on the first two axioms, that the way anything exists will be such that it can be identified in terms of spatial and temporal categories such as "here" and "now".
There is nothing in the first two axioms to pick out any categorical division over any other. We have many categories that are not universally applicable: what is the color of a thought? This is a silly question, because "color" is a category that is only useful in categorizing things that scatter or absorb electromagnetic radiation.
We have no reason to believe, on the basis of the first two axioms, that existence will be universally, unambiguously classifiable in terms of TIME and SPACE. In fact, we can be sure that only those things that obey the laws of Einstein's relativity theory, which define the concepts TIME and SPACE, will be so classifiable. We have no reason to believe that everything that exists obeys those laws. But we do have reason to believe that everything we can know about obeys them, as I'll explain in detail below.
In contrast to the first two axioms, the third axiom is much richer in content: it is a "substantial tautology."
A substantial tautology is one that entails an existential commitment. Two examples are Newtons' Second Law and the Darwinian doctrine of "Survival of the fittest."
Newton's Second Law says that force is equal to mass times acceleration. Neither force nor mass have definitions that are independent of the second law: masses are compared via the forces they exert under acceleration, and forces are compared via the amount the accelerate a mass. To say, "A exerts a force on B" is to just say that A causes B to accelerate in proportion to its mass (or would do so in the absence of opposing forces.) Likewise, to say, "A has a mass M" is just to say that under the application of a force, A accelerates at a rate proportional to M.
Neither mass nor force is independent of the other, and it seems therefore that Newton's Second Law, the foundation of physics, is a tautology and so, by the usual interpretation, vacuous. This turns out not to be the case because of the claim that force causes acceleration. For something to be a cause it must perform an action. For there to be an action there must be something that acts. The substance in Newtonian physics is the discovery of the actors, which in modern terms are fields. To be a Newtonian is to have a commitment that for every acceleration there is a field that causes the force the causes the acceleration.
Newton himself was reticent about the nature of the field that caused the gravitational force, "feigning no hypotheses" as to its nature. But he was nevertheless committed to the idea that something caused, and recent work in quantum gravity has borne out this belief.
Because Newton's second law is a substantial tautology, it is possible for it to fail, which it does in the case of electrons bound in atoms. At the end of the 19th century, the "plum pudding" model of the atom viewed electrons as stationary "raisins" and the "pudding" of positive charge that made up the bulk of the atom. Rutherford's scattering experiments made it clear that this is not the case: the positive charge of the atom was all concentrated in a nucleus that is a thousand times smaller than the cloud of electrons around it.
The problem then arose that there did not seem to be any way to keep the electrons stationary, which they had to be because otherwise, by the laws of electrodynamics, they would have radiated away all their energy and come to stop, falling into the atomic core under the force of attraction from the positively-charged nucleus. As they manifestly did not fall into the nucleus, something had to be holding them up: to a Newtonian, there had to be another field acting on the electrons to hold them in place.
No such field could be found. In particular, if there were such a field we would expect it to act on other charged particles passing by the atom, such as those in Rutherford's scattering experiments. No evidence of such a field appeared anywhere. It was as if the electrons in the atom were acted on by a field that they alone felt. Thus, the Newtonian tautology required a belief in something that had no other manifestation, a field that only acted on bound electrons and not free electrons or any other particles. Rather than describe the world in terms of such a chimeral entity, physicists found it simpler to understand the nature of the atom in terms of new dynamical laws: quantum mechanics.
A second example of a substantial tautology is the Darwinian notion of "Survival of the fittest." Critics of evolutionary theory sometimes claim that this statement is a vacuous tautology: whatever survives is by definition the fittest. But this is to miss the substance of the tautology: the connection between fitness and survival is causal, so "Survival of the fittest" entails a commitment to finding out how the concrete features of individuals contribute to their superior ability to reproduce. If features exist--and persist--that are demonstrably not conducive to an organism's reproductive success, then the doctrine of "Survival of the fittest" would be called into question, and speculations about divine favor and special creation would gain some credence.
There is no doubt that this is axiomatic in the sense that to deny it requires you to accept it. You can hardly in the absence of contradiction argue, "I do not exist" or "I am not aware of anything that exists." But notice that it does not entail that you are aware of everything that exists: it is perfectly possible to argue without contradiction, "I am not aware of everything that exists."
But there's much more to it than that: "I am aware of some things that exist" entails important existential commitments. For example, you can't argue, "I do not exist IN TIME." That is, you are a temporal being--you act and actions take place temporally, they are classifiable or categorizable unambiguously in temporal terms. Likewise, actions can be given unambiguous, though possibly distributed, spatial categorizations. That is, they have spatio-temporal identity.
Making an argument is an action, so you can't make an argument that you aren't the kind of being that acts, which means you can't make an argument that you don't exist in space and time. It is therefore axiomatic that your consciousness can be identified in spatio-temporal terms.
Ray's analysis of the concept PERSON [Ray99] is essentially an extended defense of this kind of claim about consciousness. We could as well replace the third axiom with "You are a person", which would make the axiomatic character of our existential commitments clear. To say, "I am not a person" is self-refuting because the very possibility of making the claim or engaging in argument entails accepting most of the features of personhood Ray defends:
A living human being with a mind capable of memory, abstraction, environmental interaction, and causal efficacy with respect to bodily and psychological attributes, and persistent self-awareness with regard to all of these activities and traits.So unlike the first two axioms, consciousness commits us to substantial existential claims that are much narrower than the first two axioms. In particular, it commits us to the claim that our consciousness exists in a way such that we can identify it unambiguously in time and space. This accords well with our experience: we experience ourselves HERE and NOW.
Consciousness is therefore more limited than existence and identity. It is clear that things may exist and have identity, in accordance with the first two axioms, but not exist and have identity in such a way as to admit of unambiguous classification by a consciousness in spatio-temporal terms. Our commitment to being conscious, which is undeniable, also commits us to being conscious in space and time.
Space and time, like all categories, are the product of the way we are as much as they are the product of what we categorize. We find them useful in part because they capture something important to us about mind-independent reality. We find them necessary because they are required for the kind of consciousness we have: a consciousness that is capable of acts of awareness. For consciousness to act, it must act in space and time. If we could be aware without action, we would not have this constraint. But that is not the kind of consciousness we are.
Everything we know about the physics of the brain suggests that the "here" and "now" of consciousness are the "here" and "now" of special relativity. That is, when I say that consciousness is in time and space, I mean the time and space as understood in terms of special relativity.
The photon pair described in the experiment above can be seen as a non-local entity. We can think of it as two separate photons connected by some influence that results in the kind of correlation that is observed between polarization measurements on each member of the pair.
My purpose in the rest of this discussion is to give an account of this influence in conceptualist terms, without imputing reality to any particular category used for classification over and above the reality of the particulars that are subsumed under the category by a conscious subject. In particular, TIME and SPACE will be treated as names of mind-dependent abstractions, not as real abstract features of existence.
What is required, then are local principles that our categorization of reality must conform to if reality is to be understood by consciousness. These principles are the laws of thought, and there are two:
Identification by consciousness is, for the reasons given above, necessarily local identification.
To the extent that it is nonlocal, it therefore does not admit of identification by a conscious subject. It is not possible to identify (categorize) the nonlocal aspects of reality in such a way as to make our identifications obey the laws of thought.
On this account, it is apparent that quantum mechanics is an attempt to capture the local consequences of nonlocal aspects of existence. It is an attempt to create a set of local categories we can use to identify aspects of existence that are not local. The well-known "weirdness" of quantum mechanics, its resistance to realist interpretation and ambiguous relationship to classical physics (which is local) is a result of this.
The aspects of existence underlying quantum phenomena are constrained by the axioms: they exist, and they exist in some way. But they do not conform to the conditions required by the laws of thought. They do not admit of unambiguous identification in spatio-temporal terms.
This is a problem for realism, because according to realism universals have exactly the same kind of existence as particulars, and so it would be impossible for there to be universals (the categories of nonlocal reality) that are not graspable by consciousness. This would be like have particulars that have an influence on other particulars, but are not in any way perceptible. But conceptualists understand universals as made things, and in particular things made by conscious subjects for their own purposes. It is no surprise to a conceptualist that some aspects of reality are such that they are not susceptible to spatio-temporal categorization. To a conceptualist it is not that there are categories that cannot be known, but rather aspects of reality that cannot be categorized. If things exist that don't conform to requirements of the laws of thought, then a conceptualist should be content to not try to categorize them.
The most important is that Kant eschewed any possibility of knowing anything about mind-independent reality, about "things as such." But the experiment described above tells us something very important about mind-independent reality: it is nonlocal. This single fact, the legacy of John Bell, is the death-knell of the Kantian program.
Given the existence of a single fact about mind-independent reality, we are justified in asking what else we might learn about it. Any future metaphysics to come forth as a science will not have a prolegomena written by Kant, because this is precisely the kind of program that he argued was impossible.
The nature of the conceptualist argument is also quite different from Kant's who was obviously not motivated by questions about two-photon correlation experiments.
Is this necessarily the case?
There are several sense in which this question can be taken. One is in terms of physics, where we might ask if there is anything in this argument that could lead us to predict the value of Planck's constant. How such an argument could be formulated is not entirely clear, but it would take as its starting point the condition that if something is unknowable to one observer, it must be unknowable to all observers. This is the condition that mind-independent reality must be independent of all minds. Future work will focus on this possibility, although it seems like a pretty tenuous idea.
Another sense in which this question can be taken is to ask about the relationship between being and change that has dominated metaphysics since the pre-Socratics. Is there any sense in which the nonlocality of mind-independent reality is necessary for the world of being and change that we experience?
In particular, the randomness that is such a prominent characteristic of quantum mechanical phenomena can be seen as a result of nonlocal reality. Although it is obscured by the usual statements of the theory, every particle emitted in a quantum mechanical process can be viewed as a member of a correlated pair. When we say an atom emits a single photon, for instance, we should view the photon as being correlated with the source atom until something interacts with one or the other of them to destroy the correlation. It seems likely that the nonlocal connection between source and particle is related to the randomness of the emission process, though of course how the two are related is impossible to say, because to do so would require us to categorize nonlocal reality.
But it is curious that the stable, persistent world we experience seems to be built on such a random, wildly fluctuating foundation. Yet we might wonder if the stability we experience necessitates the randomness beneath it. A useful analogy in this regard is that of commodities markets. Prices experienced by consumers of bread, for example, are extremely stable. Yet the reason for this is the existence of wheat futures, which are traded at very volatile prices, and it is necessary for this volatility to exist for the stable prices consumers experience to exist. Without the volatility of commodities markets, stable consumer prices would not exist. We might ask if the randomness of quantum phenomena are equally necessary for the stable existence of the world of experience.
"Non-causal" is usually interpreted to mean "random" or "indeterminate" or "irregular", but it is not at all clear that this is the correct way of looking at it in this case. "Causality" as defined here is a relation between things that can be categorized by us in spatio-temporal terms. Because mind-independent reality cannot be so categorized, its relations cannot be causal, but this is not to say that there are no relations at all. There does not seem to be any suitable language for expressing the nature of these relations, but the stability and regularity of the world makes it clear that they are at the very least determinate, although in what terms this determinate aspect can be stated I cannot say. The strict enforcement of the law of conservation of angular momentum, for example, indicates the determinate nature of these relations, but beyond that there seems to be very little that can be said about them.
The great advantage of conceptualism in this situation is that it allows us to understand why it is that we cannot categorize some modes of existence--those that are subsumed under the concept NONLOCAL--without forcing us to abandon the idea of mind-independent reality. Armed with this understanding, we can move beyond the realist task of trying to find out how mind-independent reality "really is" and ask instead if there are other categories, as well as "nonlocal" that we can subsume it under. It is clear from the discussion above of the nature of relations in mind-independent reality that we will probably have to create new categories, or radically alter old ones, in pursuit of this goal, but this has always been the manner in which scientific understanding of the world has progressed.
Two of the most basic categories of experience are space and time. These are concepts abstracted from our experience of reality and of our own mental processes. Locke argues that we come to understand TIME by our awareness of the succession of ideas in our consciousness. Likewise, we come to understand SPACE by an awareness of relations between ourselves and reality. Our will causes us to interact with things--when I stand up and walk about I realize that while there is something about my experiences that stays the same, there is something that changes. As I move my feet in particular ways the world changes--some parts of my visual fields expand, others contract. I eventually learn to abstract these changes and ascribe them to changing spatial relationships between me and reality, rather than ascribing them to reality changing independently of me. That is, I recognize that the appearance of reality is relative to me, and spatial concepts such as POSITION and DISTANCE describe an important aspect of that relationship.
An alternative to the analysis above, of course, is that there is a force that acts on the world such that things that I would normally describe as "far away" are getting squeezed to make them smaller, and as I move my feet in a way that I would normally say makes me approach them the strength of the force decreases and so they expand. It may even be possible to work out a consistent physics based on such a force. But it wouldn't be very parsimonious. The alternative understanding that appearances are relative to the observer is vastly simpler.
Before Einstein, various odd features of electrodynamics were explained by something much like the mysterious force in the preceding paragraph. It was assumed that as objects moved more or less quickly through something called the "aether", which was supposed to permeate the universe, they were acted on by forces that caused them to shrink in the direction of motion. It turns out that Maxwell's theory of electrodynamics implied that if objects shrank this way, then time as measured by a moving observer would appear to run more slowly.
Einstein recognized that the ordinary concept of "perspective" applied to motion as well as position, so that as well as the appearance of reality changing as we move around in it, it also changes when we speed up with respect to it. The laws of special relativity can be seen as a generalization of the ordinary concept of PERSPECTIVE. It is far simpler for us to understand that railway tracks appear to get closer together as the run off into the distance not because some force squeezes things far away from us, but because of our spatial relation to them.
Likewise, Einstein showed that it is far easier to understand that moving objects appear foreshortened and moving clocks run slowly not because of the force of the aether acting on them, but because of the rate of change of our spatial relation to them. The consequences of this generalization of PERSPECTIVE are more important than the consequences of the ordinary kind of perspective, however.
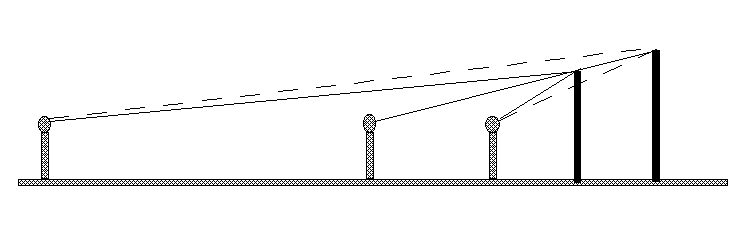
The most important consequence of special relativity is that it turns out to be impossible to define "simultaneous" for two events that are not in the same place. If two events are spatially separated, different observers will see them as happening at different times. The understand this in terms of ordinary perspective, imagine a pair of posts of different height, and two observers standing so that both observes and the posts are all in a line. To one observer, the tops of the posts may appear to line up with each other, as shown in the figure. To the other observer, one post appears to be higher than the other. To a third observer on the other side, what looks like the "tall" post to the second observer appears to be the "short" post. It's all a matter of their relative locations.
The importance for us of Einstein's extension of perspective
is that when we talk about the identity of a thing,
we need to specify when it is identified. And for
an object that is widely extended in space we have
a problem, because we would like to identify it in
terms of those edges we find useful, but we cannot
meaningfully define all the edges at the same time,
because there is no common "instant" that applies uniformly
to the entire unity bounded the the edge.
Noether's Theorem We believe angular momentum is conserved because of Noether's Theorem, which relates conserved quantities to symmetries of physical systems. In particular, angular momentum is associated with rotational invariance: if there is no preferred direction in the universe, then angular momentum is conserved. A great deal of effort has been invested in the past decade to look at this question with regard to the cosmic microwave background radiation, and no preferred direction has been found. Some extensions to general relativity suggest that there might be the possibility of small effects that would create a tiny preference for one direction over all others, but these effects are far too small to allow for the size of angular momentum conservation violation implied by non-instantaneous communication in photon-pair sources. It is worth nothing that correlated photon pairs are produced in one of the more common cosmological processes: electron-positron annihilation, so this question is not just a matter of a few special cases prepared by humans in laboratories.